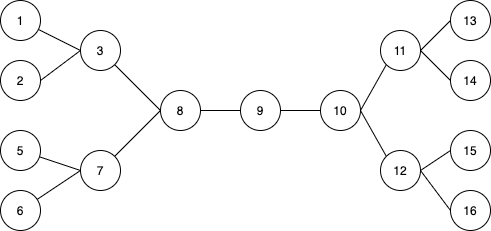
Bidirectional BFS

Posted on | In | | Total number of readers of this article times
Words count in article: 1.1k words | Reading time ≈ 6 minutes

Bidirectional BFS is applicable to the case where the target node is known; the initial node expands toward the target node and the target node expands toward the initial node at the same time, until the same node appears in both expansion directions, and the search ends. For example, in a maze, when we need to know the number of steps to reach each location, a normal BFS is sufficient, but if we only need to know the number of steps to reach a specific location, we should use a two-way BFS. Start BFS from two target points at the same time, so we will have two different queues. Update the smaller one each time until there are elements in the two queues that overlap, indicating that the path is found. For example in the following graph, it will stop at node 9.

Time Complexity

Suppose if the branching factor of the tree is b and the distance between the target vertex and the source is d, then the normal BFS search complexity will be $O(b^d)$. On the other hand, if we perform two search operations, the complexity of each search will be $O(b^{d/2})$ and the total complexity will be $O(b^{d/2} + b^{d/2})$, which is much less than $O(b^d)$.

The branch factor refers to the number of children of each node in the expanded tree, i.e., the number of new elements that can be reached by each element. For example, in a maze where you can only move up and down, the branch factor is 4.

Word Ladder

Word Ladder is a hard level question. It can be solved by using BFS. However BFS will time out. We can use Bidirectional to solve this issue.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
class Solution {
public:
    vector<vector<string>> findLadders(string from, string to, vector<string>& wordList) {
        
        unordered_set<string> lexicon(wordList.begin(), wordList.end());
        auto result = std::vector<std::vector<std::string>>{};
        
        // check whether exist to, if not just return a empty
        if (not lexicon.count(to)) {
            return result;
        }

        // init a word maps for double bfs
        auto word_maps = unordered_map<std::string, std::vector<std::string>>{};
        // the left vector
        auto left = unordered_set<std::string>{from};
        // the right vector
        auto right = unordered_set<std::string>{to};
        // contain all the visited elements
        auto visited = unordered_set<std::string>{};

        // the bfs direction, could start at from and start at end
        // true means start at from
        // false means start at end
        // this is helpful for store the word into hashmap
        auto ahead = true;
        auto found = false;

        // which contain all the words
        while (not left.empty() and not right.empty()) {
            // change the position when left > right
            // part of two end bfs algorithm
            if (left.size() > right.size()) {
                std::swap(left, right);
                ahead = not ahead;
            }

            // contain all the words which generate according to left set words
            // which like insert to queue in bfs
            auto queue = unordered_set<std::string>{};

            // insert all the left set into visited
            visited.insert(left.begin(), left.end());

            // loop all the element in the left
            for (auto origin_word : left) {
                auto neighbors = neighbor(origin_word, visited, lexicon);
                for (auto const& word : neighbors) {
                    if (std::find(right.begin(), right.end(), word) != right.end()) {
                        found = true;
                    }
                    if (ahead) {
                        word_maps[word].push_back(origin_word);
                    }
                    else {
                        word_maps[origin_word].push_back(word);
                    }
                    queue.insert(word);
                }
            }
            // put the new path to left then do new iterator
            left = queue;

            // if found the to word, then generate the word ladders
            if (found) {
                result.push_back(std::vector<std::string>{to});
                // the first one should be from
                while (result[0][0] != from) {
                    result = generate_result(result, word_maps);
                }
                break;
            }
        }

        // std::sort(result.begin(), result.end());
        return result;
    }
    
    
        /**
     * generate the neighbor words according to the word
     * to change the char from a-z
     * @param word the currecnt word to generate neighor words
     * @param visited the visited word
     * @param lexicon all the words
     * @return the neighors of the word
     */
    auto neighbor(const std::string& word,
                  const unordered_set<std::string>& visited,
                  const unordered_set<std::string>& lexicon) -> unordered_set<std::string> {
        // contains all the neighbor words
        auto words = unordered_set<std::string>{};

        for (auto i = std::vector<int>::size_type{0}; i < word.size(); i++) {
            // because we does n
            // ot want to change the current word
            // so we use curr_char to store the char which will be replaced
            char curr_char = word[i];
            // change the curr with a-z and check whether visited and whether in lexicon
            for (auto c = 'a'; c <= 'z'; ++c) {
                word[i] = c;
                // to avoid same word
                if (curr_char == c) {
                    continue;
                }

                // the word should not visited and should in lexicon
                if (not visited.count(word) 
                   and lexicon.count(word)) {
                    words.insert(word);
                }
            }

            word[i] = curr_char;
        }

        return words;
    }

    /**
     * iterate the result according to the end word
     * it can be a recurrsion, but I do not want to do that
     * recurrsion not stable.
     *
     * In the hashmap the word stored as: end->{w1, w2, w2}
     * this means w1, w2, w3 can convert to end, similar idea for start
     *
     * @param words is the result which contain as list
     * @param word_maps hashmap, key is word, values is word ladders
     * @return a new list of result and then loop again
     */
    auto generate_result(const std::vector<std::vector<std::string>>& words,
                         const std::unordered_map<std::string, std::vector<std::string>>& word_maps)
       -> std::vector<std::vector<std::string>> {
        auto temp = std::vector<std::vector<std::string>>{};

        // the word_maps were stored as a hashmap
        // key is the word, value is the word ladders
        for (auto const& word_list : words) {
            auto t = word_list[0];

            // get the related word from hashmap
            for (auto const& word : word_maps[t]) {
                // insert the value in the front of list
                auto w = word_list;
                w.insert(w.begin(), word);
                temp.push_back(w);
            }
        }

        return temp;
    }
};

This problem is also the first assignment of COMP6771 in 20T2.

----- End Thanks for reading-----