LeetCode Part 2

Posted on | In | | Total number of readers of this article times
Words count in article: 2.1k words | Reading time ≈ 13 minutes

An extension of leetcode. Keep working on leetcode.

Daily Temperatures

Daily Temperatures: Given a list of daily temperatures T, return a list such that, for each day in the input, tells you how many days you would have to wait until a warmer temperature. If there is no future day for which this is possible, put 0 instead.

For example, given the list of temperatures T = [73, 74, 75, 71, 69, 72, 76, 73], your output should be [1, 1, 4, 2, 1, 1, 0, 0].

Brute Force

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def dailyTemperatures(self, T: List[int]) -> List[int]:
        num = len(T) - 1
        data = [0]

        for i in range(len(T) - 2, -1, -1):
            if T[i] >= T[num]:
                data.insert(0, 0)
                num = i
            else:
                count = 1
                for j in range(i + 1, num + 1):
                    if T[j] <= T[i]:
                        count += 1
                    else:
                        break
                data.insert(0, count)

        return data

However, the worst time complexity is $O(N^2)$. The code can not pass one of the complex test case which is (Time Limit Exceeded).

Advance Approach

Stack can be used to improve the efficiency of this issue. We use stack to store a key-value temperature with decreasing order where key is the index of temperature, and value is the temperature. The time complexity of this approache is $O(N)$. For example:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Temperature: [73, 74, 75, 71, 69, 72, 76, 73]
stack = []
res = [0, 0, 0, 0, 0, 0, 0, 0]

1. index = 0
stack = [(0, 73)]

2. index = 1
74 > 73, pop (0, 73) and set res[0] = index - 0
stack = [(1, 74)]
res = [1, 0, 0, 0, 0, 0, 0, 0]

3. index = 2
75 > 74, pop (1, 74) and set res[1] = index - 1
stack = [(2, 75)]
res = [1, 1, 0, 0, 0, 0, 0, 0]

4. index = 3
71 < 75, add (3, 71) into stack
stack = [(2, 75), (3, 71)]

5. index = 4
69 < 71, add (3, 69) into stack
stack = [(2, 75), (3, 71), (4, 69)]

6. index = 5
72 < 69, pop (4, 69) and (3, 71), set res[4] = index - 4, and res[3] = index - 3
stack = [(2, 75), (5, 72)]
res = [1, 1, 0, 2, 1, 0, 0, 0]

7. index = 6
76 > 72 pop (5, 72) and (2, 75), set res[5] = index - 5, and res[2] = index -2
stack = []
res = [1, 1, 4, 2, 1, 1, 0, 0]

And implementation is:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def dailyTemperatures(self, T: List[int]) -> List[int]:
        stack = []
        res = [0] * len(T)

        for i in range(0, len(T)):

            while stack and stack[-1][1] < T[i]:
                index, val = stack.pop()
                res[index] = i - index

            stack.append((i, T[i]))

        return res

Minimum Size Subarray Sum

Minimum Size Subarray Sum: Given an array of positive integers nums and a positive integer target, return the minimal length of a contiguous subarray [numsl, numsl+1, …, numsr-1, numsr] of which the sum is greater than or equal to target. If there is no such subarray, return 0 instead.

Example:

1
2
3
Input: target = 7, nums = [2,3,1,2,4,3]
Output: 2
Explanation: The subarray [4,3] has the minimal length under the problem constraint.

Brute Force

The basic approach is to use two loops to solve that. The time complexity of this approach is $O(N^2)$. It will cause time limit exceeded.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        length = 9999

        for i in range(0, len(nums)):
            res = nums[i]
            if res >= target:
                length = 1
                continue
            for j in range(i + 1, len(nums)):
                res += nums[j]

                if res >= target:
                    length = min(length, j - i + 1)
                    break
        return length if length != 9999 else 0

Advance Approach


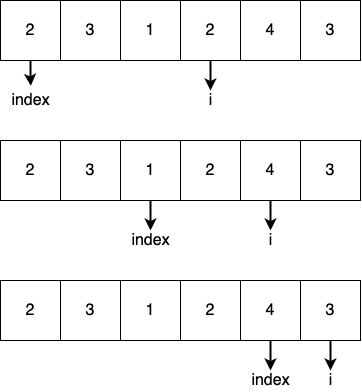
To solve this issue, we can use Sliding Window to solve this issue. This method is similar to the double pointer. The index the left index of this array. When the sum between i and index is greater or equal to the target, then advance i and index to find other positions that sum is greater or equal to the target. The basic idea of sliding windows is shown in the Figure.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        index = 0
        res = 0
        min_len = 99999999

        for i in range(0, len(nums)):
            res += nums[i]

            while res >= target:
                length = i - index + 1
                min_len = min(length, min_len)
                res -= nums[index]
                index += 1

        return min_len if min_len != 99999999 else 0

Valid Anagram

Given two strings s and t, return true if t is an anagram of s, and false otherwise.

1
2
3
4
Input: s = "anagram", t = "nagaram"
Output: true
Input: s = "rat", t = "car"
Output: false

Brute Force

This issue can be solved by using two loop. But the time complexity is $O(N)$. In addition, it also can be done through sort algorithm, to check whether same. But it is too complex. Here we did not code for this approache.

Advance Approach

We can use hashmap to record that how many times they appeared in the string. Therefore, the time complexity is $O(N)$.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution:
    def isAnagram(self, s: str, t: str) -> bool:
        if len(s) != len(t):
            return False
        
        data = {}

        for i in s:
            if i not in data:
                data[i] = 1
            else:
                data[i] += 1

        for i in t:
            if i not in data:
                return False
            else:
                if data[i] == 0:
                    return False
                else:
                    data[i] -= 1

        for key, val in data.items():
            if data[key] != 0:
                return False

        return True

Combinations

Given two integers n and k, return all possible combinations of k numbers out of the range [1, n]. You may return the answer in any order. For example

1
2
3
4
5
6
7
8
9
10
Input: n = 4, k = 2
Output:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

It is pretty hard to use loop to solve this issue. Beacause the k determine the number of nested loop, when k=2 then it should have three nested loop. However, when k in not a const number, then we can not determine how many loops we need.

Therefore, we can use recursion to do this kind of issues. We can seen it as a tree as shown in the Figure. The root node is 1-n and the deep is k. Pick up the number from left to right without repeating. We can set up a path to record the visited path, and when the length of path is equal to k then add the path to result.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        def back_tracking(n, k, index, path, result):
            if len(path) == k:
                result.append([i for i in path])
                return path

            for i in range(index + 1, n + 1):
                path.append(i)
                back_tracking(n, k, i, path, result)
                path.pop()

            return result
        
        return back_tracking(n, k, 0, [], [])

Combination Sum III

Combination Sum III: Find all valid combinations of k numbers that sum up to n such that the following conditions are true:

  • Only numbers 1 through 9 are used.
  • Each number is used at most once.

Return a list of all possible valid combinations. The list must not contain the same combination twice, and the combinations may be returned in any order. For example:

1
2
3
4
5
Input: k = 3, n = 7
Output: [[1,2,4]]
Explanation:
1 + 2 + 4 = 7
There are no other valid combinations.

This question is pretty similar with the previous one, just add one more constrain (sum = n).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        def combine(k, n, index, path, result):
            if len(path) == k:
                if sum(path) == n:
                    result.append([i for i in path])
                return path

            for i in range(index, 10):
                path.append(i)
                combine(k, n, i + 1, path, result)

                path.pop()

            return result
    
        return combine(k, n, 1, [], [])

Valid Palindrome

Valid Palindrome: Given a string s, determine if it is a palindrome, considering only alphanumeric characters and ignoring cases.

1
2
3
Input: s = "A man, a plan, a canal: Panama"
Output: true
Explanation: "amanaplanacanalpanama" is a palindrome.

This one is pretty easy, we just need to ignore the char which is not belong to a-z, 0-9. During the processing, we can use double pointer to do that. Set a index from the left and a index from the right.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def isPalindrome(self, s: str) -> bool:
        s = s.lower()
        start = 0
        end = len(s) - 1

        while start <= end:
            l = s[start]
            r = s[end]

            if not l.isalnum():
                start += 1
                continue

            if not r.isalnum():
                end -= 1
                continue

            if s[start] != s[end]:
                return False

            start += 1
            end -= 1

        return True

Next Greater Node In Linked List

Next Greater Node In Linked List is a medium problem.
We are given a linked list with head as the first node. Let’s number the nodes in the list: node_1, node_2, node_3, ... etc.

Each node may have a next larger value: for node_i, next_larger(node_i) is the node_j.val such that j > i, node_j.val > node_i.val, and j is the smallest possible choice. If such a j does not exist, the next larger value is 0.

Return an array of integers answer, where answer[i] = next_larger(node_{i+1}).

Note that in the example inputs (not outputs) below, arrays such as [2,1,5] represent the serialization of a linked list with a head node value of 2, second node value of 1, and third node value of 5.

Approach

This problem is pretty similar with Daily Temperatures which can be solved by applying stack. For this issue, we can use stack + hashmap to solve it with $O(n)$ time complexity.

  1. Init stack and the final result.
  2. result(hashmap) will recored the index as key and greater or 0 value as the value
  3. When the temp node value is greater then the top value of the stack, update the result value and pop the top value of stack.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def nextLargerNodes(self, head: ListNode) -> List[int]:
        stack = []
        result = {}
        
        temp = head
        index = 0
        
        # stack store like (val, pos)
        while (temp != None):
            
            while len(stack) != 0 and temp.val > stack[len(stack) - 1][0]:
                result[stack[len(stack) - 1][1]] = temp.val
                stack.pop(len(stack) - 1)
            
            stack.append((temp.val, index))
            result[index] = 0
            
            index += 1
            temp = temp.next
        
        
        return result.values()

We can use the following data to give an example:

1
2
Input: [2,1,5]
Output: [5,5,0]

In the following part, we will display the result and stack storage.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1. stack.push((2, 0)) stack = [(2, 0)], result = {0: 0}

2. stack.push((1, 1)), stack = [(2, 0), (1, 1)], result = {0: 0, 1: 0}

3. The node value is 5, greater than 1, then
    1. top value of stack is (1, 1), then result[1] = node.val (5), stack pop (1, 1)
    2. top value of stack is (2, 0), then result[0] = node.val (5), stack pop (2, 0)
    3. End while loop, and insert the (5, 3) into stack and result.

The final value in result is:
result = {
    0: 5,
    1: 5,
    2: 0
}

How Many Numbers Are Smaller Than the Current Number

How Many Numbers Are Smaller Than the Current Number is an easy problem. Howerver, it is more interesting than other questions.

Given the array nums, for each nums[i] find out how many numbers in the array are smaller than it. That is, for each nums[i] you have to count the number of valid j’s such that j != i and nums[j] < nums[i].

Example 1:

1
2
3
4
5
6
7
8
Input: nums = [8,1,2,2,3]
Output: [4,0,1,1,3]
Explanation: 
For nums[0]=8 there exist four smaller numbers than it (1, 2, 2 and 3). 
For nums[1]=1 does not exist any smaller number than it.
For nums[2]=2 there exist one smaller number than it (1). 
For nums[3]=2 there exist one smaller number than it (1). 
For nums[4]=3 there exist three smaller numbers than it (1, 2 and 2).

Approach

Naive approach is brute force. Just use two nest loop can get the result.

1
2
3
4
5
6
7
result = []
for i in range(0, len(nums)):
    num = 0
    for j in range(i, len(nums)):
        if nums[i] > nums[j]:
            num += 1
    result.append(num)

The time complexity is O(n^2)

----- End Thanks for reading-----