In math, prime numbers are whole numbers greater than 1, that have only two factors – 1 and the number itself. Prime numbers are divisible only by the number 1 or itself. For example, 2, 3, 5, 7 and 11 are the first few prime numbers.

Brute Force

For this solution we can use two loops to handle. For example, we want to find all the prime number between 2 and 100, then we can write code like this:

num = 100
primes = []

for i in range(2, num):
    for j in range(2, i):
        if i % j == 0:
            break
    else:
        primes.append(i)

The time complexity is $O(n\sqrt{n})$. But when the number is huge, then it is very slow. There is a small optimization in the method.

num = 100
primes = []

for i in range(2, num):
    for j in range(2, i // 2 + 1):
        if i % j == 0:
            break
    else:
        primes.append(i)

Ehrlich Sieve Algorithm

The algorithm enumerates all the numbers from small to large, and for each prime number, it sifts all its multiples, and the rest is the prime number. The time complexity is $O(loglog(n))$.

primes = []
is_prime = [True] * (num + 1)

for i in range(2, num):
    if is_prime[i]:
        primes.append(i)
        for m in range(1, num // i + 1):
            is_prime[i * m] = False

Performance Evaluation

We set the value of num to [10000, 50000, 100000, 200000]. For Brute Force (BF) we used its optimization algorithm. For Ehrlich Sieve (ES) we do not change anything.

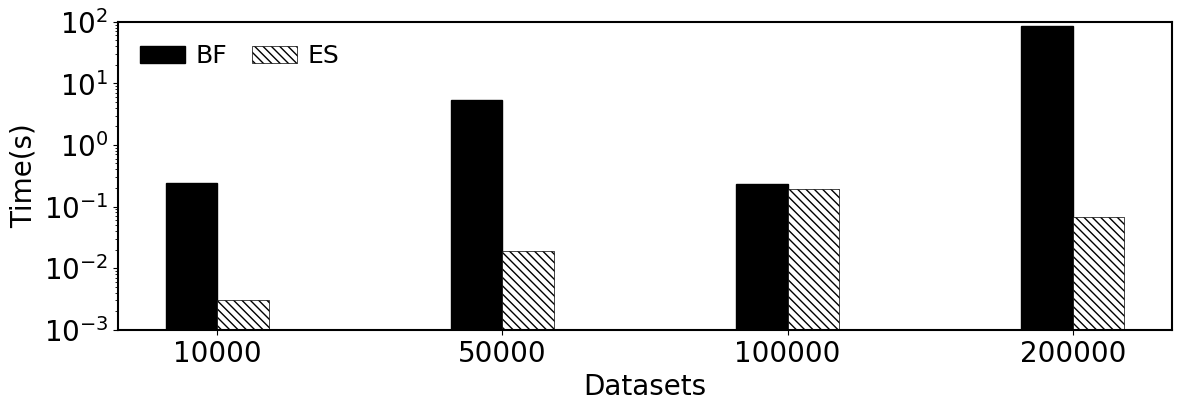
We can see that as the number increases the time consumed by BF is higher. For all the test, the time cost of ES algorithm no more than one seconds.