Union-Find Set

Posted on | In | | Total number of readers of this article times
Words count in article: 441 words | Reading time ≈ 2 minutes

In computer science, a disjoint-set data structure is a data structure used to handle the merging and querying of disjoint sets (a series of sets with no duplicate elements).

Structure

A non-intersecting forest represents each set as a tree (deepth with 1), where each node is an element. A node holds a reference to its parent node, and the root node of the tree holds an empty reference or a reference to itself or some other invalid value to indicate itself as the root node. This data structure was first proposed by Bernard A. Galler and Michael J. Fischer in 1964,but it took several years before a precise analysis was completed. As shown: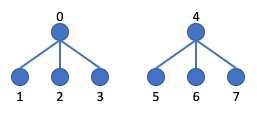

New Approach

There are many different types of variations of this data structure that we can change to suit different needs. I used two HashMap to store the roots and parent (parent and roots). For parent, it stores the roots of every element, for roots, it stores the root of all the elements.
parent can be seen as {node: root}, roots can be seen as {root: [node1, node2, ...]}.

In my method, I use Hashmap to store the tree. So, the search complexity is $O(n)$.

1
return parent[x]

Union

For union, we need to set the root of such element to be a new root. And merge the childs of such root.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def union(x, y):
    rootX = parent[x]
    rootY = parent[y]

    if rootX == rootY:
        return
    
    parent[y] = rootX
    roots[rootX] += roots[y]

    for n in roots[y]:
        parent[n] = rootX
    
    del roots[y]

Application

It can be used for subgraph pattern matching decompistion, bipartite graph and commuity.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
class UF:
    def __init__(self):
        """
        :param parent {node: root}
        :param roots: {root: [n1,n2..]}
        """
        self.parent = {}
        self.roots = {}

    def init(self, n):
        for i in range(0, n):
            self.parent[i] = i
            self.roots[i] = [i]

    def union(self, p, q):
        rootP = self.parent[p]
        rootQ = self.parent[q]

        if rootP == rootQ:
            return

        self.parent[q] = rootP
        self.roots[rootP] += self.roots[q]
        del self.roots[q]

    def find(self, x):
        """
        to find x parent
        :param x:
        :return:
        """
        if x in self.parent:
            return self.parent[x]

        return -1

    def isConnect(self, p, q):
        """
        check whether two val has same root
        :param p:
        :param q:
        :return:
        """
        rootP = self.find(p)
        rootQ = self.find(q)

        return rootP == rootQ

    def getRoots(self):
        return self.roots.keys()

    def getRecords(self):
        return self.roots


if __name__ == '__main__':
    uf = UF()
    uf.init(10)
    uf.union(0, 1)
    uf.union(1, 2)
    uf.union(2, 3)

    uf.union(5, 6)
    uf.union(4, 5)
    x = uf.find(3)

    print(x)
----- End Thanks for reading-----